https://es.calameo.com/read/005184854991e6843db84

Limites indeterminados 

En muchas ocasiones se presenta el cálculo de límites de cocientes, diferencias y productos de funciones en los que al reemplazar la variable por el valor al cual tiende se generan indeterminaciones del tipo 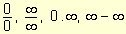. El resultado de estos límites no 

puede anticiparse y el mismo puede ser cero, ¥ , -¥ , un número finito diferente de cero, o bien puede no existir. Para resolverlos, se realizan procedimientos algebraicos adecuados que permitan salvar la indeterminación.

Limites infinitos

Una función f(x) tiene por límite +∞ cuando x → a, si fijado un número real positivo K > 0 se verifica que f(x) > k para todos los valores próximos a a.

Limites exponenciales

 Nos referimos aquí no a límites de la forma  Lim  , con g(x) teniendo por límite , cuyo resultado simplemente es 1, sino a límites de la forma:

Lim 

cuando f(x) tiene por límite 1, y g(x) tiene por límite .  Vamos a tomar el EJEMPLO 1, para describir minuciosanente el proceso:

límite que es de la forma indicada. Para su resolución debe tenerse en cuenta que:

   

como igualdad fundamental. O en forma más general:

siendo g(x) una expresión que tiende bien a + ó  bien a - , en el infinito.

  En concreto para resolver el límite del ejemplo 1 deberemos pasarlo a esta forma del número e , siguiendo para ello los siguientes pasos:

a) Separación del numerador en dos partes, una de ellas idéntica al denominador.

b)  Expresar el parentesis en la forma ( 1 + f/g).   

c) Pasar el numerador f al denominador como cociente (1+1/(g/f)).   

d)  Asegurarnos de que (f/g) tiene por límite + ó  -, entonces multiplicar y dividir al exponente por ese (f/g).

e) Con ello hemos conseguido (1+1/(g/f)) elevado a (g/f), lo cual es el número e. Finalmente, el resultado será e elevado al (límite del) exponente dividido entre (g/f): -En nuestro ejemplo este (g/f) es (x-5/2):

http://youtu.be/lp-ydcRLTOE?hd=1

Diapositivas en calameo.

https://es.calameo.com/read/005104804b9f5c3a8b077

¿Quien invento el valor absoluto?

Técnicamente, Jean-Robert Argand surgió con la idea de valor absoluto, aunque refería específicamente a complejo valor absoluto. Sin embargo, fue quien ideó la notación Karl Weierstrass
 | x | en 1841.

Historia de valor absoluto.

Valor absoluto

En matemáticas, el valor absoluto o módulo de un numero real es su valor numérico sin tener en cuenta su signo, sea este positivo (+) o negativo (-). Así, por ejemplo, 3 es el valor absoluto de +3 y de -3.

El valor absoluto está relacionado con las nociones de magnitud, distancia y norma en diferentes contextos matemáticos y físicos. El concepto de valor absoluto de un número real puede generalizarse a muchos otros objetos matemáticos, como son los cuaternarios, anillos ordenados, cuerpos o espacios vectoriales.

                                               

Definición

El valor absoluto se define en cualquiera de los sistemas numéricos, de los números enteros, racionales, reales como:

• |a| = a si a ≥ 0;

• |a| = -a en otro caso; para un elemento a de los sistemas numéricos indicados.